Time Series Forecasting Techniques in Python
This one's gonna be a bit long, but I hope to explain Time Series Analysis in a way that you'll remember it for a long time. I will begin by telling you about what we're gonna cover in this article:
Table of Contents
- What is Time-Series and why is it important?
- How do we load and visualize Time-Series data in Python?
- What are the important components of a Time-Series?
- How do we test for stationarity in a Time-Series?
- What are different ways to remove trend and seasonality in a Time-Series?
- What are different Time-Series forecasting models that you might end up using?
- What is ACF and PACF?
- How to forecast a Time-Series?
- Finally, how do we evaluate the accuracy of a Time-Series?
1. What is a Time Series?
Now you all know what time-series is, but I'll explain it anyway. A time-series data is one where you collect the data with a timestamp. For example:
- Collecting energy production data of a power plant. Now you can collect data points like 50 kWh, 76 kWh, 49 kWh, 55 kWh, but they won't make much sense unless you have a timestamp associated with it. 50 kWh on May 28 2020, 76 kWh on May 27 2020, 49 kWh on May 26 2020, 55 kWh on May 25 2020, see? Now you know that these energy values are energy produced on the given days.
- Customer transactions from Walmart, Costco, StopnShop etc. You want to know what did a customer purchase and when did he/she do that.
- Number of visits on a website. Without a date associated with, they'll all be just flying numbers.
You get the jist!
This type of data is critical because time is an important predictor of actions in these cases. For example:
- With increasing population and electricity reaching more and more people, the demand will increase over time. Also, electricity demand goes up in the summers as everybody want to sit in an AC room. If you don't know at what time the data is collected, you'd lose all that critical information.
- People tend to buy a lot during Black Friday sales and Christmas vacations. This can help you understand how would the sales of the next year might look like. Also, you can analyze what items were most famous and predict the sales of them individually too.
- If you're running a sports blog, you will have highs and lows in the number of visits on your blog, depending on the seasons when sports is at the peak. But, you would also want to understand the overall pattern and what can be the visitors count the next year, to plan something new or big for your blog.
For the purpose of this article, I am using the energy production data of a solar PV system in India. The data is real and is provided by TrackSo, by permission of the owner of the PV system.
Some brief about the data
- The data is the total energy generated by the solar system since the time it was installed
- The data is collected remotely using TrackSo's IoT hardware that sends data to its cloud IoT platform for monitoring and analysis
- The data is collected at 10 minute frequency (but it's not exact, may vary a little due to the fact that it uses GPRS connection to transfer the data from the hardware to the platform)
- We will aggregate this data into daily data to predict energy production for the next 3 days
2. Load and Visualize
Please download the datafile from here and put it somewhere on your drive. Then mount your drive by clicking 'Mount Drive' button on the left pane of your notebook and you're ready to go.
energy_data = pd.read_csv('/content/drive/My Drive/Colab Notebooks/TrackSo Energy Forecasting/energy_data.csv')
energy_data.tail()
NOTE: Please change the location of file as per your drive location.
The above command is gonna show you the last 5 records of the time series data:
When you read the data, the timestamp column will be read as a 'object' datatype. You can convert it by using:
energy_data.timestamp = pd.to_datetime(energy_data.timestamp)
energy_data.info()
You can plot the dataset to see how it looks. Since it is the total energy produced by a solar PV system since its installation, it should start from near 0 to the energy produced as of May 29, 2020. If you see the tail, you'll see the the energy value starts from 680.64 kWh and that means that it would have taken a few days for us to start monitoring the plant.
This makes sense, right? Because this is the 'Total Energy' generated by a system over time, hence it should be an always increasing value. But you can see that it's not perfectly linear.
Now we are interested in the 'Daily Energy' as we want to forecast energy produced in a day for the next 'n' days. We can do it in 2 ways:
- Subtract the max value of a day with it min value
- Subtract the max value of a day with the max value of the previous day
Having experienced multiple issues with data collection from remote systems around the world, I had to be aware of what method can give the best results. There are multiple problems while collecting data from such systems:
- Sometimes the data-logger stops sending data because of bad internet connection
- Other times, it is switched-off for some reason
- And yet other times, it is damaged and it takes some time to get it repaired or replaced.
So there are chances that you do not have 100% smooth data over time. Let's try to make 'Daily Energy' using both ways:
# get the date component out of the timestamp to group by date
energy_data['date'] = energy_data.timestamp.dt.date
# group by date and get the max and min valueThe above code will give you a data frame as shown below:
daily_energy_data = energy_data.groupby('date').agg({"value": [np.max, np.min]})
daily_energy_data.reset_index(inplace=True)
daily_energy_data.columns= ['date', 'max_te', 'min_te']
daily_energy_data.head()
Let's create 'Daily Energy' using our first way, i.e. max_te - min_te
daily_energy_data['daily_energy_1'] = daily_energy_data.max_te - daily_energy_data.min_te
daily_energy_data.head()
daily_energy_data['daily_energy_2'] = daily_energy_data.max_te.diff()
daily_energy_data.head()
- The value are matching exactly in the screenshot above, but that might not be the case in all the rows.
- There's no value for 2018-07-28 in 'daily-energy_2' column. That's because the value in that row can't take a diff() from the previous day value. So, it NaN.
Let's plot the daily energy parameters that we just created. You can use the same code to visualize that we used above:
figure(num=None, figsize=(20, 5), dpi=80, facecolor='w', edgecolor='k')
plt.plot(daily_energy_data.date, daily_energy_data.daily_energy_1)
plt.title('Daily Energy Produced', fontsize = 16)
plt.xlabel('Timestamp')
plt.ylabel('Energy (kWh)')
figure(num=None, figsize=(20, 5), dpi=80, facecolor='w', edgecolor='k')
plt.plot(daily_energy_data.date, daily_energy_data.daily_energy_2, color = 'orange')
plt.title('Daily Energy Produced', fontsize = 16)
plt.xlabel('Timestamp')
plt.ylabel('Energy (kWh)')
figure(num=None, figsize=(20, 5), dpi=80, facecolor='w', edgecolor='k')
plt.plot(daily_energy_data.date, daily_energy_data.daily_energy_2)
plt.plot(daily_energy_data.date, daily_energy_data.daily_energy_1)
plt.title('Daily Energy Produced', fontsize = 16)
plt.xlabel('Timestamp')
plt.ylabel('Energy (kWh)')
Do you see that spike in the daily energy calculated using the 2nd way? That's what I'm talking about. The points, somewhere in November 2019 are 0. Meaning, there was no energy produced in those days. Let's plot the data only for last 3 months of 2019.
figure(num=None, figsize=(20, 5), dpi=80, facecolor='w', edgecolor='k')
plt.plot(daily_energy_data[(daily_energy_data.date >= np.datetime64('2019-10-01')) & (daily_energy_data.date <= np.datetime64('2019-12-31'))]['date'],
daily_energy_data[(daily_energy_data.date >= np.datetime64('2019-10-01')) & (daily_energy_data.date <= np.datetime64('2019-12-31'))].daily_energy_2)
plt.plot(daily_energy_data[(daily_energy_data.date >= np.datetime64('2019-10-01')) & (daily_energy_data.date <= np.datetime64('2019-12-31'))]['date'],
daily_energy_data[(daily_energy_data.date >= np.datetime64('2019-10-01')) & (daily_energy_data.date <= np.datetime64('2019-12-31'))].daily_energy_1)
plt.title('Daily Energy Produced', fontsize = 16)
plt.xlabel('Timestamp')
plt.ylabel('Energy (kWh)')
plt.grid()
There seem to be some problem with data from November 15 and November 25, 2019. Let's see how it looks:
daily_energy_data[(daily_energy_data.date >= np.datetime64('2019-11-15')) & (daily_energy_data.date <= np.datetime64('2019-11-25'))]
So here's the problem:
- There's no energy generated on 18st, 21st and 23rd of November.
- Where you see 0 value, the max energy of day before will not match the min energy of given day. They should match, right? Because no energy is produced during the night. So the value on the night before, should be the value on the next morning.
- In order to fix that, wherever we see the min_te = max_te, we need to max_te of given day with the min_te of the next day. This will hopefully reduce some of the missing data problems.
The following code fix that problem for us:
# changing the values
for index, row in daily_energy_data.iterrows():
if row.max_te == row.min_te:
daily_energy_data.loc[[index], 'max_te'] = daily_energy_data.loc[[index+1], 'min_te'].values[0]
# recalculating the values
daily_energy_data['daily_energy_1'] = daily_energy_data.max_te - daily_energy_data.min_te
daily_energy_data['daily_energy_2'] = daily_energy_data.max_te.diff()
daily_energy_data.head()
Let's plot the data again for that duration first:
figure(num=None, figsize=(20, 5), dpi=80, facecolor='w', edgecolor='k')
plt.plot(daily_energy_data[(daily_energy_data.date >= np.datetime64('2019-10-01')) & (daily_energy_data.date <= np.datetime64('2019-12-31'))]['date'],
daily_energy_data[(daily_energy_data.date >= np.datetime64('2019-10-01')) & (daily_energy_data.date <= np.datetime64('2019-12-31'))].daily_energy_2)
plt.plot(daily_energy_data[(daily_energy_data.date >= np.datetime64('2019-10-01')) & (daily_energy_data.date <= np.datetime64('2019-12-31'))]['date'],
daily_energy_data[(daily_energy_data.date >= np.datetime64('2019-10-01')) & (daily_energy_data.date <= np.datetime64('2019-12-31'))].daily_energy_1)
plt.title('Daily Energy Produced', fontsize = 16)
plt.xlabel('Timestamp')
plt.ylabel('Energy (kWh)')
plt.grid()
Problem gone! Both the data values match now. Let's plot the whole data and see if that looks ok too.
figure(num=None, figsize=(20, 5), dpi=80, facecolor='w', edgecolor='k')
plt.plot(daily_energy_data.date, daily_energy_data.daily_energy_2)
plt.plot(daily_energy_data.date, daily_energy_data.daily_energy_1)
plt.title('Daily Energy Produced', fontsize = 16)
plt.xlabel('Timestamp')
plt.ylabel('Energy (kWh)')
plt.grid()
Looks OK!
Now, let's remove the columns that we don't need:
Let's move on to understand the components of a time-series.
3. Components of a time-series
Any time-series may be decomposed into 3 components:
- Long term trend (up or down)
- Seasonality (calendar based movements, like high energy production in summer and lower in winters, though that's not always true)
- Irregularity (or the noise. This is unsystematic short term fluctuations in the data that may or may not be explained)
NOTE: You may or may not have all these components in your time-series at the same time.
Before we talk about these components, we should discuss about STATIONARITY.
What's STATIONARITY?
A time-series is called stationary when its statistical parameters (which mean, variance, standard deviation etc.) remain constant over time. For a time-series to be called stationary, it should basically have the following conditions met:
- Constant Mean
- Constant Variance
- Constant autocorrelation
Like we have some assumptions when we do a regression analysis, we need to have these assumptions tested on a time series to be able to implement any statistical method for forecasting/modelling.
There are ways to identify if a time-series is stationary or not. For example, the following time-series is not stationary and we can visually see that. It has an overall increasing trend and if you plot it's rolling mean and. standard deviation, it would look something like the second graph:
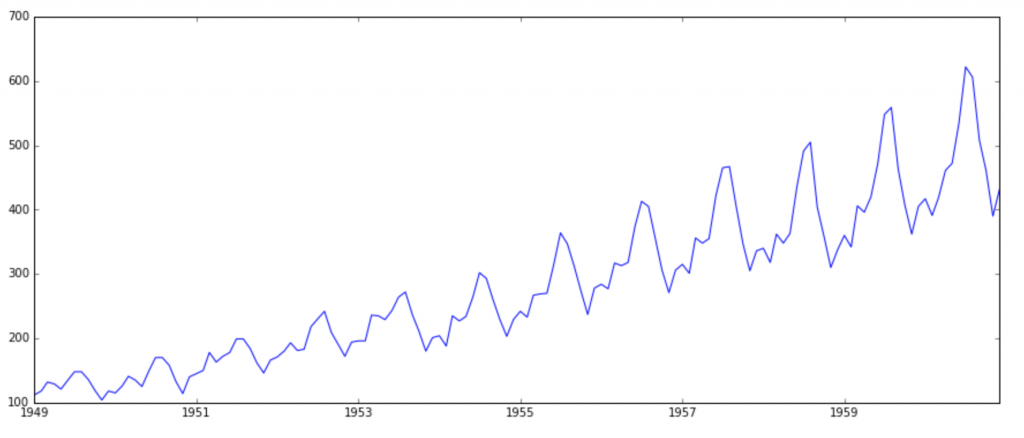
In our case, it's difficult to visually identify if the series is stationary or not. Let's try and plot the rolling mean and rolling standard deviation of our time-series:
def rolling_stats(timeseries):
# Calculating rolling statistics
rolling_mean = timeseries.rolling(90).mean()
rolling_std = timeseries.rolling(90).std()
#Plotting rolling statistics
figure(num=None, figsize=(20, 5), dpi=80, facecolor='w', edgecolor='k')
orig = plt.plot(timeseries, color='lightgray',label='Original')
mean = plt.plot(rolling_mean, color='orange', label='Rolling Mean')
std = plt.plot(rolling_std, color='brown', label = 'Rolling Std')
plt.legend(loc='best')
plt.title('Rolling Mean & Standard Deviation')
plt.show(block=False)
rolling_stats(daily_energy_data)
But visual analysis is not always right and obvious. In this case, we should also try and do some statistical test to see if our time series in stationary or not. There are multiple statistical tests that can be done to test stationarity. The most commonly used test is the Dickey-Fuller test. It's a type of unit root test that defines how closely a time-series is defined by the trend.
To do a statistical test, we need to set out hypothesis:
Ho = The series in NOT stationary
Ha = The series is stationary
You need to understand what test are you using to test stationarity and then define your hypothesis.
Let's do that test now:
from statsmodels.tsa.stattools import adfuller
def dicky_fuller(timeseries):
#Perform Dickey-Fuller test:
print('Dickey-Fuller Test Results:')
dftest = adfuller(timeseries['daily_energy'], autolag='AIC')
dfoutput = pd.Series(dftest[0:4], index=['Test Statistic','p-value','#Lags Used','Number of Observations Used'])
for key,value in dftest[4].items():
dfoutput['Critical Value (%s)'%key] = value
print(dftest)
dicky_fuller(daily_energy_data)
Results:
Dickey-Fuller Test Results:
Test Statistic -2.403829
p-value 0.140659
#Lags Used 13.000000
Number of Observations Used 658.000000
Critical Value (1%) -3.440327
Critical Value (5%) -2.865942
Critical Value (10%) -2.569114
dtype: float64
How do we interpret this?
- The 'Test Statistic' should be greater than at least any one of those critical values. Only then you can say with that Critical Value (x%) confidence that the time-series in stationary.
- The p-value should be smaller than the alpha (which is 0.05 generally).
In our case, none of the conditions meet. So we cannot reject the NULL hypothesis.
Trend
If you observe the number of visitors on Facebook since its inception, you'll see a graph faintly similar 'Total Energy' i.e. increasing over time. This means that the trend of the series was positive. This also means that the time-series in not STATIONARY.
Seasonality
As you'll notice that every year, the number of people going to Disneyland increase a whole lot during the summer vacations. That means, every year, when you see a time series of number of people visiting Disneyland, you'll see an extra jump in the graph. That's seasonality. Seasonality also makes a time series NON STATIONARY, as we saw in the graphs and tests above.
You'll notice in the graph below that there seem to be a dip in around November and then a jump in energy production in around May-June. This makes sense because that's winters and summers in India, respectively.
Constant Autocorrelation
Autocorrelation means that any value in a timeseries is dependent on a lagged value of the same timeseries. That means: energy value at 't' is dependent on energy value at 't-k' where k can be any lag value. This condition asks that this autocorrelation be constant.
In order to make a time series stationary, we need to remove the above discussed components from it and then model on the stationary series. Once we do that, we can then add the trend and seasonality back into the forecasted values to get the final output. Simple?
I'll talk about that in the 2nd part of this article!
Cheers!
Nitin
















Comments
Post a Comment